Area is a measure of how much space there is inside a shape. Calculating the area of a shape or surface can be useful in everyday life – for example you may need to know how much paint to buy to cover a wall or how much grass seed you need to sow a lawn.
This page covers the essentials you need to know in order to understand and calculate the areas of common shapes including squares and rectangles, triangles and circles.
Calculating Area Using the Grid Method
When a shape is drawn on a scaled grid you can find the area by counting the number of grid squares inside the shape.
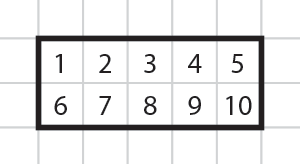
In this example there are 10 grid squares inside the rectangle.
In order to find an area value, using the grid method, we need to know the size that a grid square represents.
This example uses centimetres but the same method applies for any unit of length or distance. You could, for example be using inches, metres, miles, feet etc.

In this example each grid square has a width of 1cm and a height of 1cm. In other words each grid square is one 'square centimeter'.
Count the grid squares inside the large square to find its area..
There are 16 small squares so the area of the large square is 16 square centimeters.
In mathematics we abbreviate 'square centimeters' to cm2. The 2 means ‘squared’.
Each grid square is 1cm2.
The area of the large square is 16cm2.
Counting squares on a grid to find the area works for all shapes – as long as the grid sizes are known. However, this method becomes more challenging when shapes do not fit the grid exactly or when you need to count fractions of grid squares.

In this example the square does not fit exactly onto the grid.
We can still calculate the area by counting grid squares.
- There are 25 full grid squares (shaded in blue)
- 10 half grid squares (shaded in yellow) – 10 half squares is the same as 5 full squares.
- There is also 1 quarter square. (¼ or 0.25 of a whole square).
- Add the whole squares and fractions together: 25 + 5 + 0.25 = 30.25.
The area of this square is therefore 30.25cm2 .
You can also write this as 30¼cm2.
Although using a grid and counting squares within a shape is a very simple way of learning the concepts of area it is less useful for finding exact areas with more complex shapes, when there may be many fractions of grid squares to add together.
Area can be calculated using simple formulas, depending on the type of shape you are working with.
The remainder of this page explains and give examples of how to calculate the area of a shape without using the grid system.
Areas of Squares and Rectangles (and parallelograms).
The simplest (and most commonly used) area calculations are for squares and rectangles.
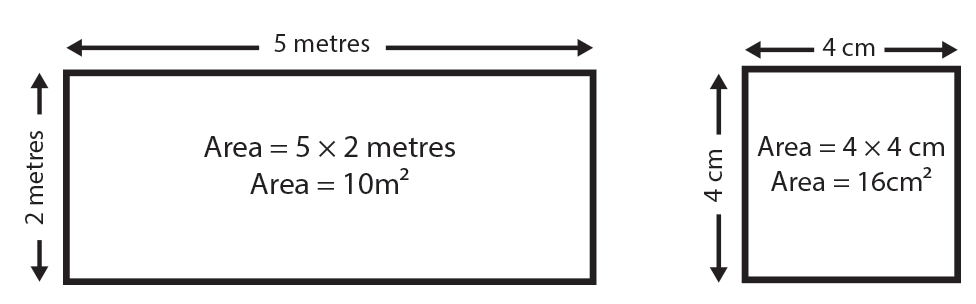
To find the area of a rectangle multiply its height by its width.
For a square you only need to find the length of one of the sides (as each side is the same length) and then multiply this by itself to find the area. This is the same as saying length2 or length squared.
It is good practice to check that a shape is actually a square by measuring two sides. For example the wall of a room may look like a square but when you measure it you find it is actually a rectangle.
Often, in real life, shapes can be more complex. For example, imagine you want to find the area of a floor, so that you can order the right amount of carpet.
A typical floor-plan of a room may not consist of a simple rectangle or square:

In this example, and other examples like it, the trick is to split the shape into several rectangles (or squares). It doesn’t matter how you split the shape - any of the three solutions will result in the same answer.
Solution 1 and 2 require that you make two shapes and add their areas together to find the total area.
For solution 3 you make a larger shape (A) and subtract the smaller shape (B) from it to find the area.
Read more at: https://www.skillsyouneed.com/num/area.html